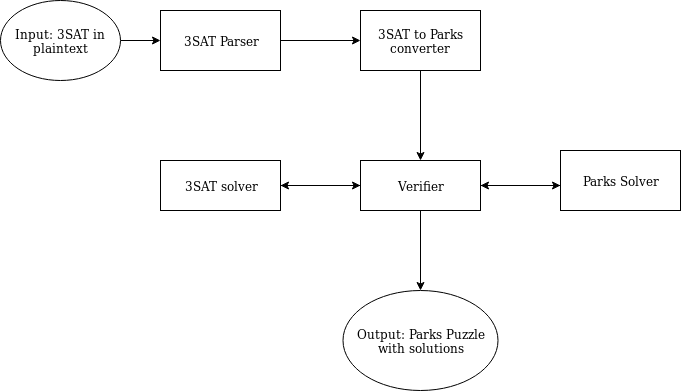
CS488-Week14-Update
This week I mostly worked on the final video, as well as making some small final touches to the paper based on Charlie’s suggestions.
CS488-Week13-Update
I mostly worked on my poster during this week. There were a number of small issues with my original poster created using LaTeX, which I could not fix without delving into a lot of code, so I recreated it using power point and improved it based on Charlie’s feedback. Igor, my advisor, also pointed out a number of improvements that could be made to my paper, so I worked on an intermediate draft for additional feedback before I complete the final version.
CS488-Week12-Update
I worked on the feedback I received from Igor concerning some of the difficult notation, and overall organization of my paper. I also removed some obvious lemmas and simplified the basic results for the second draft.
CS488-Week11-Update
I worked on presenting the proof in the most succinct way possible for the poster. I worked on several iterations and finally narrowed down on what is the current first draft. I also received feedback on the first draft of my paper from Charlie, and discussed the paper as well as Charlie’s feedback with Igor.
CS488-Week10-Update
I spent this week on finishing up a very detailed proof that Parks is NP complete. I also worked on improving the exposition of ideas leading up to the main result in my paper, which really helped me with the software video.
CS488-Week9-Update
I did not get to do much due to the various disruptions caused by Corona virus. I am currently working on getting things in order and figuring out meeting times with my adviser and whatnot.
CS488-Week8-Update
I am currently working on a proof that non-contiguous kPARKS is NP-Complete. I am also mostly done with my paper.
CS488 – Elevator Pitch
Parks Puzzle is a popular puzzle game that is played on a square grid. A Parks Puzzle consists of an nxn grid with contiguous regions known as parks. The aim of the puzzle is to place trees within parks such that every row, column, and park contains one tree, and no two trees are on squares that border one another. My senior proposal is to show that the associated problem of deciding whether a given configuration of a Parks puzzle is consistent with a solution or not, dubbed PARKS, is NP-Complete. This result lets us meaningfully state that the Parks Puzzle in general is an NP-Complete problem, and that it is highly unlikely that there exist any polynomial time algorithms for the problem. Since I have already found a proof, I am currently working on the kPARKS problem, which is the analogous problem of placing k trees in each row, column and park.
CS488-Week7-Update
Now that I have a proof for the parks puzzle, I am spending time working on a more general puzzle that we’ve dubbed kPARKS, which is the analogous problem of placing k trees in every row, column and Park. I am also working on writing the proof and the results that build up to the proof in a clean and concise manner.
CS488-Week6-Update
This week I worked on finalizing my proof for the IFF and OR gadgets, and rewriting the final proof for the paper draft. I am now planning on working on an explicit algorithm for the reduction for use in the program.
CS488-Week5-Update
The proof has been completed. This week I will work on writing it out rigorously, as well as designing the program.
CS488-Week4-Update
This week I took a short break from working on the proof to start working on the app. I am currently trying to figure out whether it is worth designing the Parks app as a webapp, while also starting work on some of the basic modules.
CS488-Week3-Update
I worked with possible ways of proving that non-contiguous Parks is NP-Complete, and found one good avenue for exploration. Over the week I produced a general technique to convert any instance of 3-SAT to an instance of the non-contiguous Parks Puzzle, thus proving that it is NP-Complete, our first major result. I am working to modify the proof, or try similar techniques for the contiguous case this week.
CS488-Week2-Update
Over this week I finished up an non-contiguous IFF and OR gadgets, however I came to the conclusion, after meeting with Igor, that there does not seem to be a way to effectively put together these two gadgets. However, we also concluded that in most cases, it is not a particularly difficult challenge to find a gadget for contiguous parks, if one already knows the equivalent gadget for contiguous parks. Since I have reached a dead end, over the next week I am going to try out one promising new direction, and hopefully by close to proving the result for non-contiguous parks within the next two weeks.
CS488-Week1-Update
This was the first week so I worked on getting back up to speed with the research, and on creating presentations for the first class.
CS388-Week16-Update
I finished my final proposal and I’m rechecking everything for submission this week.
CS388-Week11-Update
I only worked on finishing the first draft of the proposal this week.
CS388-Week10-Update
I finished a first pass of all but one of the papers in my reading list, and also read some of the papers that are highly relevant to my project, which I had already read for a first pass, for a second or third pass depending on how relevant the content seemed. I have also outlined the introduction and motivation for my project, and am working through the related works section. Apart from the project proposal, I have also spent some time trying to find some ‘gadgets’ that will assist with the proof for a simpler variant of parks puzzle, which is an effort that has not yet borne much fruit.
CS388-Week9-Update
I went over the broad categories that need to be addressed by the project proposal, and created a proposal outline for Assignment 7. I also worked with my advisor, Igor, to find a good candidate for the reduction adn start working on the proof. We found that there was a natural way of reducing a subset of 3SAT, 2SAT with distinct variables was, to an instance of Parks Puzzle. For next week I hope to generalize the technique to a larger subset of 3SAT.
CS388-Week8-Update
This week I worked on improving my understanding of the Parks Puzzle and exploring possible proof techniques to show that it is NP complete from two directions. I continued working on the Time Complexity chapters of “Introduction to The Theory of Computation” by Michael Sipser to round out my theoretical understanding, while also solving many instances of the puzzle using an app on my phone. I came onto one general idea for the proof involving only ‘AND’ and ‘OR’ gadgets that I discussed with my advisor, who made some suggestions involving an ‘IFF’ gadget, which I am going to continue working on. I also received feedback on my literature review, which showed some significant problems that I corrected according to the grading rubric.
CS388-Week6-Update
This week I spent some time finalizing my proposal idea. I discussed the Parks Puzzle with Igor and come to the conclusion that I should work on proving its NP-Completeness for my final project. I had to discuss this idea with my advisor Igor, as well as Charlie and Xunfei before I could finalize this plan. Once I had this confirmed by Xunfei, I put aside my work on the other ideas and started to solely focus on NP-Completeness. My first task is to go through the relevant chapters of “Introduction to The Theory of Computation” by Michael Sipser nad working through problems to clear up my understanding of the problem, which I have started to work on.
CS388-Week5-Update
I found a very promising paper called “an introduction to the conjugate gradient method without the agonizing pain” and started working through it. I have only gotten through the first 10 pages or so, but it is helping me think of narrower research questions. I have also skimmed through a fair number of NP-completeness reductions, and have a much better idea about the background work I will need to do to be able to work on the Parks Puzzle problem. Some especially strange and interesting reductions I have come across are a reduction of SAT to minesweeper and a reduction of the Hamiltonian cycle problem for cubic graphs to the zen garden puzzle, which use boolean ‘gadgets’ and nodes and edges that can be combined to create instances of the game.
CS388-Week4-Update
I have pretty much decided on my main topic, which is working on the complexity of the Parks Puzzle. I found a survey paper that goes over a number of puzzle problems, and provides a vast reading list, which I am working through now.
CS388-Week3-Updates
Idea #1
Name of Your Project Computational complexity of the ‘Park Puzzle’
What research topic/question your project is going to address? The Park Puzzle is a game that involves splitting a n*n grid into different colored continuous ‘parks’. A solution to a park puzzle involves marking the position of a tree in each park such that no two trees share a row or a column. The research topic involves exploring various algorithms for solving the park puzzle, and determining some bounds on the computational complexity of the puzzle. The most involved version of this project could be to prove those bounds. (The initial, intuitive hypothesis is that the park puzzle cannot be solved in polynomial time)
Update: I am looking into the proofs of NP-completeness of other pencil puzzle problems to gain an understanding of the techniques involved in proving such complexity bounds.
Idea #3
Name of Your Project Fast Integer multiplication
What research topic/question your project is going to address? There have been significant improvements in algorithms for fast multiplication of integers within the last decade (see Fast integer Multiplication by Anandya et al), approaching O(nlogn), which use modular arithmetic and computation on p-adics The research project would be to explore the theory behind these algorithms and verify their results.
Update: I am looking into the minimal mathematical background required to make sense of how the algorithms work, without necessarily getting into all of the details.
Idea#3 Iterative solvers for systems of Linear Equations
Description Large and sparse systems of linear equations appear in the solution to some partial differential equations by finite difference methods, and in general many day-to-day problem areas such as in engineering and scientific computing. As such the theory of developing methods for solving such large systems, and proving their correctness is an area of active research. in this project I would like to test the effectiveness of various iterative methods at finding solutions to systems linear equations with various characteristics by taking an experimental approach.
Update: no update for this idea
CS388 – Week2 – Three Ideas
Changes to Idea #1
There were no major changes recommended, except that the scope of the project could be limited to classical iterative solvers of linear systems.
Idea #2
Name of Your Project Computational complexity of the ‘Park Puzzle’
What research topic/question your project is going to address? The Park Puzzle is a game that involves splitting a n*n grid into different colored continuous ‘parks’. A solution to a park puzzle involves marking the position of a tree in each park such that no two trees share a row or a column. The research topic involves exploring various algorithms for solving the park puzzle, and determining some bounds on the computational complexity of the puzzle. The most involved version of this project could be to prove those bounds. (The initial, intuitive hypothesis is that the park puzzle cannot be solved in polynomial time)
What technology will be used in your project?A simple Java program for generating park puzzles coded by Igor (similar apps are also available online). Pen and lots of paper.
What software and hardware will be needed for your project? If computational methods seem like the appropriate way to tackle the problem, then the appropriate software may be written in python for reasonably sized puzzles
How is your project different from others? What’s new in your project? The project is more research oriented, and the end result is not a concrete implementation of an idea as a program.
What’s the difficulties of your project? What problems you might encounter during your project? It is quite likely that the problem is very complex, and a more restricted scope in the same direction might have to be chosen.
Idea #3
Name of Your Project Fast
multiplication using p-adics
What research
topic/question your project is going to address? There
have been significant improvements in algorithms for fast
multiplication of integers using p-adic numbers, approaching
O(nlogn). The research project would be to explore the theory behind
these algorithms and verify their results.
What
technology will be used in your project? C++
for writing the algorithms
What software and hardware
will be needed for your project? Cluster
for testing the algorithms
How is your project
different from others? What’s new in your project? It
is quite similar to the first idea I had proposed, but involves a
different area of mathematics.
What’s the
difficulties of your project? What problems you might encounter
during your project? I expect
most of the difficulties to arise with understanding and analysing
the algorithms.
CS388 – Week 1 – First Idea
- Name of Your Project Iterative solvers for systems of Linear Equations
- What research topic/question your project is going to address? The effectiveness of various iterative methods at finding solutions to systems linear equations with various characteristics. Taking experimental / numerical analysis perspectives.
- What technology will be used in your project? C++ for implementing the solvers.
- What software and hardware will be needed for your project? Cluster, or some other computer with sufficient memory for the testing.
- How are you planning to implement? Choose a class of iterative solvers and test them against various types of matrices.
- How is your project different from others? What’s new in your project? It is closer to some of the more theory oriented projects, but leans heavily towards applied mathematics.
- What’s the difficulties of your project? What problems you might encounter during your project? The theory of iterative solvers is quite heavy on numerical analysis, which might limit the scope of the project to a a further restricted class of solvers.